分散と標準偏差の求め方｜ばらつきを見る統計の基本をやさしく解説

はじめに

「データの中心」は平均値で見られますが、
「データがどれくらいバラバラか？」を表すには、分散と標準偏差が欠かせません。

このページでは、統計の基礎である 「分散」と「標準偏差」の意味と計算方法を、くま先生と一緒にやさしく学びます。
数式が苦手な人にもわかるよう、図や具体例を交えて丁寧に解説します！

データの「ばらつき」ってどう見るの？

分散とは？｜データのばらつきを示す指標

**分散（variance）**とは、データが平均からどれくらい離れているかを表す数値です。
すべてのデータについて「平均からの差の2乗」をとり、その平均を出します。

計算式（母分散）：

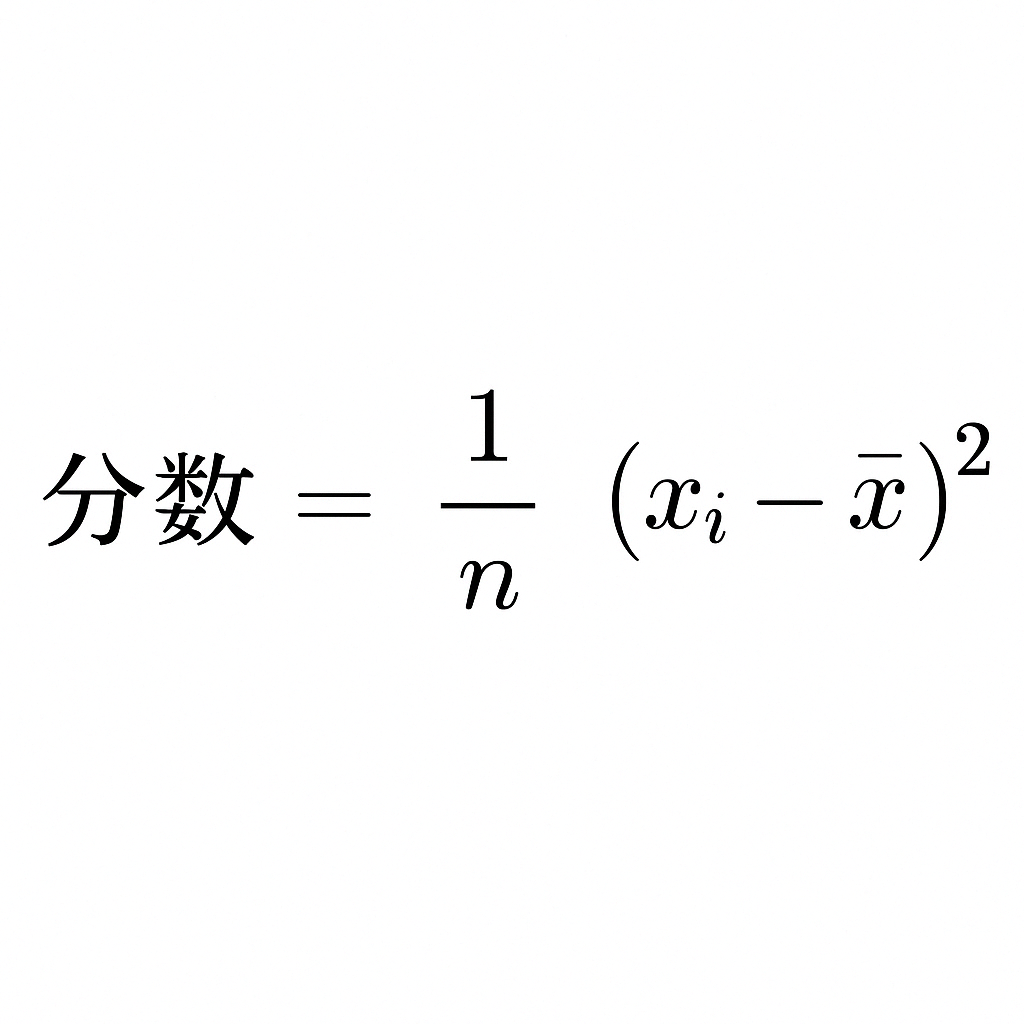
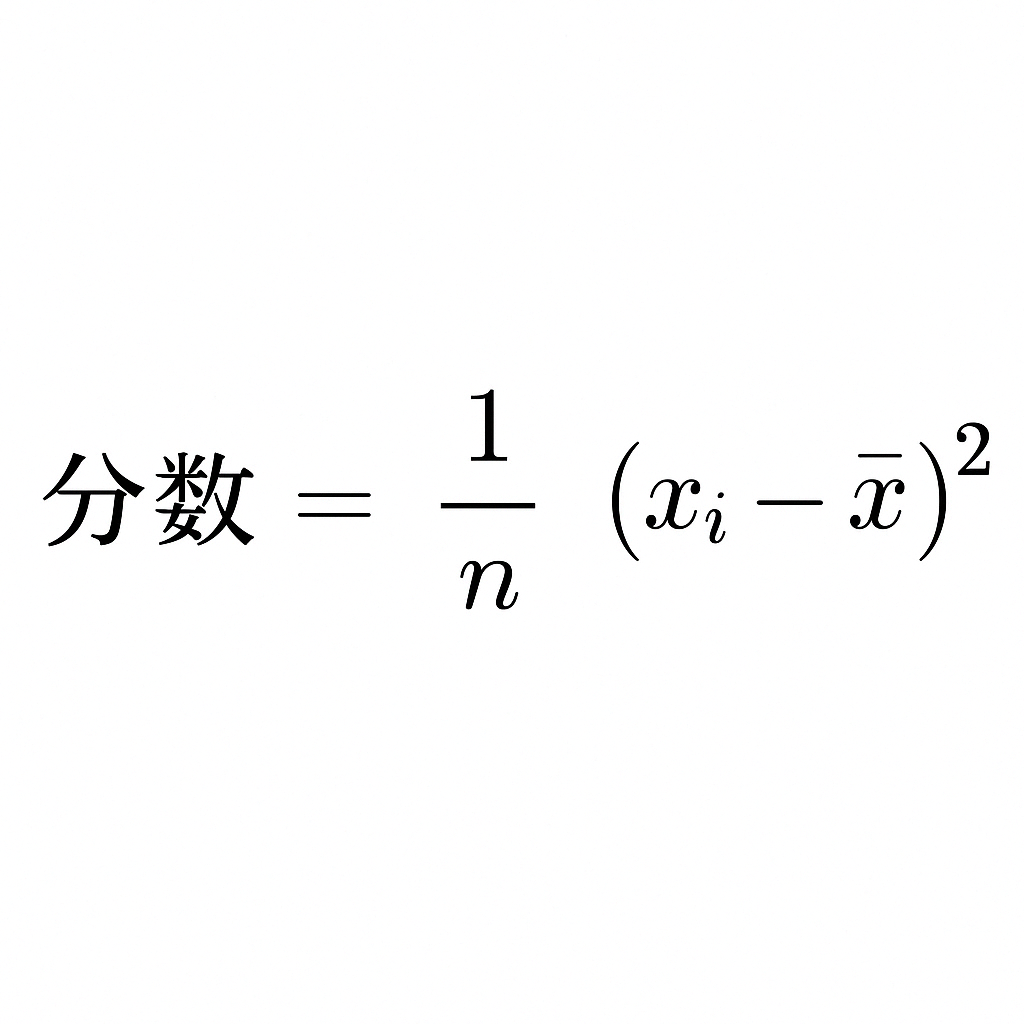
例：データ【70, 80, 90】

• 平均 = 80
• 平均との差 = -10, 0, +10
• 差の2乗 = 100, 0, 100
• 分散 = (100 + 0 + 100) ÷ 3 = 66.7

ポイント：

• 数値が大きい → データが広がっている
• 数値が小さい → データがまとまっている

標準偏差とは？｜分散の「単位を戻した」値

**標準偏差（standard deviation）**は、分散の平方根です。
分散は2乗の世界なので、元のデータと単位が違ってしまうという問題があります。

→ その単位を戻すために「√分散」をとったものが標準偏差です。

さきほどの例：分散 = 66.7
→ 標準偏差 = √66.7 ≒ 8.16

ポイント：

• 単位が元のデータと同じなので、直感的に理解しやすい
• 医療、看護、教育、経済など、幅広い分野で使われる

分散・標準偏差の使いどころ

シーン	指標	理由
患者の血圧のばらつき	標準偏差	平均だけでなく変動の大きさも把握できる
学生のテスト成績の安定性	分散・標準偏差	安定しているか？バラバラか？を見たい
臨床試験のばらつき評価	標準偏差	実データとの比較がしやすい

なぜ「2乗」するの？

平均との差をそのまま足すと、正と負が打ち消しあって 0 になってしまいます。
→ そこで、2乗して“正の値”にすることで、ばらつきを正しく反映しているのです。

分散・標準偏差をEZRで求めるには？

EZRでは、[記述統計] → [基本統計量の表示] から、平均・分散・標準偏差を簡単に算出できます。

※詳しい操作は別記事：EZRでの基本統計量の表示方法 をご覧ください。　→　▶作成中です。

まとめ｜平均だけじゃダメ。ばらつきも見よう！

指標	内容	使い方
分散	平均からのズレの2乗の平均	広がりを数値で評価
標準偏差	分散の平方根（単位は元と同じ）	実際のズレ感覚がつかみやすい

次に読むおすすめ記事

• 仮説検定の基本 →　▶作成中